Para enseñar a los niños desde los 7 años como mi nieto Jesús David hasta los de mas añitos, de 50 o más, he escrito esta entrada de cómo interpretar y aplicar los algoritmos requeridos par armar rápidamente, en pocos segundos, un cubo Rubik de 2 x 2, el más sencillo de todos los que se consiguen en el mercado de juguetes. Les enseño además las técnicas de memorización a partir de historias visuales utilizando mi código de memorización. Espero ustede se diviertan como yo. Aprovechemos el tiempo de vacaciones en pasatiempos lúdicos. Un cubo Rubik 2x2 de buena calidad se consigue en Colombia por cerca de diez mil pesitos.
Veamos algunas ideas preliminares sobre la algoritmia básica que he extraido de la web:
"Un computador es parecido a un niño, en el sentido de que para que haga algo, primero debemos enseñarle a hacerlo. Así por ejemplo, si queremos que un niño aprenda a cruzar la calle él "solito", le daremos una serie de instrucciones:
1º Si hay un semáforo, esperar a que se ilumine un hombrecito verde y cruzar rápidamente.
2º Si no hay un semáforo cerca, buscar un paso cebra y si está cerca hacer lo siguiente:
2.1. Ir al paso cebra.
2.2. Esperar a que no pase ningún vehículo
2.3. Cruzar.
3º. Si no hay ningún paso cebra cerca, entonces hacer lo siguiente:
3.1. Mirar a la izquierda y a la derecha para ver si viene algún coche a alta velocidad o está muy cerca.
3.2. Si no viene ningún coche cruzar rápidamente, en caso de que venga algún coche esperar e ir al paso
Si al niño no le damos todas estas instrucciones, no sabrá cómo cruzar o podría ser peligroso.
Un programa se realiza de igual forma, se deben especificar un conjunto de instrucciones (o sentencias) simples, ordenadas en una secuencia que el computador debe cumplir. El computador, al igual que el niño, entiende solamente instrucciones simples; es decir, con poco nivel de dificultad. El programa debe estar grabado en el disco duro o memoria del computador".
El Cubo Rubik se llama así porque fue creado por Enro Rubik, escultor y arquitecto húngaro, mientras se desempeñaba como maestro en la Escuela de artes en Budapest. Su pretensión era establecer un modelo lúdico para ilustrar sus clases de geometría descriptiva.

Fue inventado en 1974, y es un rompecabezas mecánico del cual existen diferentes versiones.
Uno de los más sencillos es el cubo de 2 X 2, compuesto por sólo 8 cubos, y al cual le dedicamos la atención en esta entrada del blog. Mi intención es netamente de órden pedagógico, convencido que la lúdica es la mejor forma de aprender y sobre todo de investigar. Ya lo dijo el gran Albert Einstein: "El juego es la forma más elevada de investigación"
Sobre el cubo de Rubik se han efectuado estudios serios como el realizado por Miguel Abreu García como tesis de grado en Ingeniería de Informática:
http://e-archivo.uc3m.es/bitstream/handle/10016/13264/PFC_Miguel_Abreu_Garcia.pdf?sequence=1
Existen muchos tutoriales y videos en vía a soluciones rápidas, pero el que fué mas significativo para el autor de este blog se refiere al denominado método Ortega:
https://www.youtube.com/watch?v=eWa49i9X4hM
En procura de entender los algoritmos para realizar los movimientos adecuados es indispensable interpretar la siguiente notación:
Después de analizar el video del Método Ortega para solucionar el cubo 2 x 2, el autor de este blog llegó a la siguiente conclusión:
1. Inicialmente debe armarse la corona, o parte superior del cubo con sus colores adecuados en sus cuatro bandas laterales, lo cual se logra en forma muy fácil, sin recurrir a algoritmos especiales:
Si la cara superior del cubo es la amarilla la opuesta en el caso de mi cubo 2 x 2 es la negra, en otros cubos puede ser la blanca.
2. Después de tener la corona correctamente, se presentan 9 casos o situaciones al analizar la cara opuesta a la superior. (La negra para mi cubo 2 x 2) .
Para cada caso se utiliza un algoritmo.
Veamos los nueve casos, observando los cuadros negros en la cara posterior, opuesta a la amrilla, y los cuadros negros en sus cuatro bandas laterales.
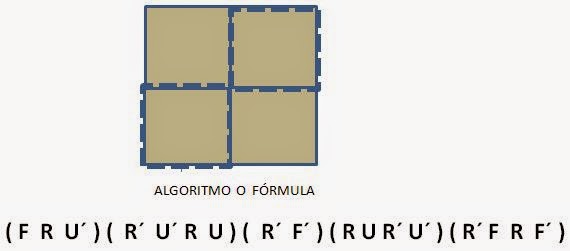
El allgoritmo o fórmula se aplica tomando el cubo como se muestra en cada figura, donde la cara superior (UP) es la negra.
CASO 1: QUEDA UN SÓLO CUADRO NEGRO EN LA CARA OPUESTA A LA AMARILLA Y TRES EN LAS BANDAS LATERALES EN LA POSICIÓN INDICADA:
CASO 2: QUEDA UN SÓLO CUADRO NEGRO EN LA CARA OPUESTA A LA AMARILLA Y TRES EN LAS BANDAS LATERALES EN LA POSICIÓN INDICADA:
CASO 3: NO QUEDAN CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, SINO EN LA POSICIÓN INDICADA EN LAS BANDAS LATERALES
CASO 4: NO QUEDA CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, SINO EN LA POSICIÓN INDICADA EN LAS BANDAS LATERALES
CASO 5: QUEDAN DOS CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, Y DOS EN LA POSICIÓN INDICADA EN LAS BANDAS LATERALES
CASO 6: QUEDAN DOS CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, Y DOS EN LA POSICIÓN INDICADA EN LAS BANDAS LATERALES
CASO 7: QUEDAN DOS CUADROS NEGROS DIAGONALMENTE EN LA CARA OPUESTA A LA AMARILLA, Y DOS EN LA POSICIÓN INDICADA EN LAS BANDAS LATERALES
CASO 8: QUEDAN LOS CUATRO CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, Y CUATRO CUBOS CORRECTAMENTE POSICIONADOS
CASO 9: QUEDAN LOS CUATRO CUADROS NEGROS EN LA CARA OPUESTA A LA AMARILLA, Y DOS CUBOS EN DIAGONAL CORRECTAMENTE POSICIONADOS
Complemente los algoritmos con el video que recomendé y disfrutará con el cubo Rubik 2 x 2. Por lo general al armar la corona superior, el cubo queda en uno de los primeros 7 casos. De allí puede ser necesario luego ir al caso 8 o 9. ¡ Y el cubo queda perfectamente posicionado !
Mi nieto Jesús David Carvajal Ruiz , de 7 añitos, ya se está familiarizando con los algoritmos.
.Pienso que es un forma de lograr que los niños aprecien y valoren la matemática, que es la ciencia que permite crear los algoritmos a partir del razonamiento lógico y creativo
. La idea es inculcar el amor a los niños por la matemática, la lógica, el razonamiento.
Veamos ahora como aplicar la memoria visual para no utilizar el papel para aplicar los algoritmos, sino hacerlo de memoria.
Cada caso lo asociamos a una palabra de acuerdo al código de memorización que se ha explicado en otras entradas de este blog así:
Caso 1: ATILA
Caso 2: GANSO
Caso 3: TREN
Caso 4: BURRO
Caso 5: DIOS
Caso 6: ANZUELO
Caso 7: CIEGO
Caso 8: BOLA DE BILLAR
Caso 9: LLUVIA
Se procede luego a elaborar una historia lo más extraña posible asociando la palabra del código con el algoritmo o fórmula de cada uno de los 9 casos posibles para armar el cubo.
Veamos las 9 historias que se me ocurrieron: El lector puede cambiarla a su gusto.
Otra historia puede ser imaginarnos inicialmente los gansos ReuniDOS RUgiendo estruendosamente, y luego para la segunda parte de la historia los gansos entran en silencio al recordar que ellos llevan una vida muy rural ( RU´R´al) , vida relativa al campo.
Podemos también darnos cuenta que si unimos los algoritmos de los CASOS 7(ciego) y 6(anzuelo) podemos lograr el algoritmo del caso 9.
La siguiente figura puede entonces ayudarnos a recordar el caso 9:
Bajo la lluvia se observa a un ciego cuyo bastón tiene forma de anzuelo.
Espero memorice cada uno de los algoritmos de acuerdo al proceso visual que le he indicado, y se sorprenda así mismo y luego a sus amistades armando el cubo de Rubik.
A mis 67 años soy un niño grande que no deja de jugar. El gran escritor irlandés George Bernard Shaw, premio Nobel de Literatura en 1925 tiene una frase famosa: " El hombre no deja de jugar por que se haga viejo, sino es todo lo contrario, se hace viejo porque deja de jugar"



























.jpg)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
